Le Cube Soma

VERS 1936, le danois Piet Hein (1905-1996) inventait un puzzle composé de 27 cubes assemblés en sept pièces, tous les polyèdres non convexes formés de trois ou quatre cubes contigus: sont rejetés les alignements de trois ou quatre cubes ainsi que le carré de quatre cubes.

2020.02 — Description plus explicite des pièces pour les navigateurs en mode texte.

Description des pièces

1  1
1

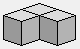
1  1  1
1

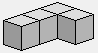
1  1  1
0  1

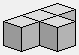
1  1
0  1  1

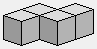
1  1
2

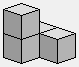
2
1  1

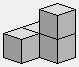
2  1
1

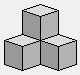
Le cube et ses variantes

3  3  3
3  3  3
3  3  3

Il existerait 240 façons différentes d'assembler les sept pièces en un cube de 3×3×3, et l'une des solutions permettrait au cube de ne pas se défaire si on le mettait en équilibre sur un de ses sommets… mais ce n'est pas le propos ici. Plutôt qu'une solution, un conseil tout à fait général: assembler les pièces les plus complexes (5, 6 et 7) en premier lieu, pour terminer par les pièces 1 et 2, plus simples à placer.

3  3  3
3  0  3  2  1
3  3  3

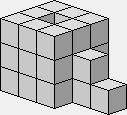
Si vous évidez un des axes du cube (comme si vous enleviez le trognon carré d'une pomme cubique), vous récupérez trois unités que vous pouvez utiliser pour monter sur le bord de la citerne. Une grande règle: chaque fois que vous avez réalisé une forme, essayez des variantes…

Contrairement au «Rubik's cube» qui ne connaît qu'une solution, le «Cube Soma» ne connaît que les limites de votre imagination et de vos possibilités de voir dans l'espace. Un beau cadeau éducatif, car on peut développer ces capacités.

5  4  3
4  3  2
3  2  1

Cet assemblage vous paraîtra peut plus facile si vous le considérez comme une autre variante du cube.

Les figures creuses

2  2  2  2  2
2  1  1  1  2
2  2  2  2  2

Voici une des rares autres figures creuses possibles, pas nécessairement facile pour des débutants. Il existe un fond à cette baignoire.

2  2  2  2
2  0  1  2
2  1  1  2
2  2  2  2

Baignoire à trou.

2  2  2  2
2  0  0  2
2  0  0  2
2  0  0  2
2  2  1  2

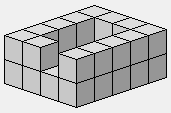
Cet enclos, ou bassin ébréché, n'a pas de fond

Les surfaces

2  1  1  1  2
1  1  1  1  1
1  1  0  1  1
1  1  1  1  1
2  1  1  1  1

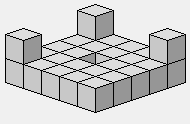
Trois pièces ont une épaisseur de deux cubes. Une figure plane aurait donc nécessairement au moins trois dépassements.

2  1  1  1  2
1  1  1  1  1
1  1  1  1  1
1  1  1  1  1
2  1  1  1

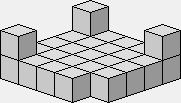
2  1  0  1  2
1  1  1  1  1
1  1  1  1  1
1  1  1  1  1
2  1  0  1  2

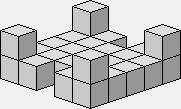
1  1  1  1
2  1  1  1  1
2  1  1  1  1  1
2  1  1  1  1
1  1  1  1

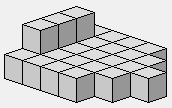
2  1  1  1  1  1  1  1  1
1  2  1  1  1  1  1  1
1  1  2  1  1  1  1

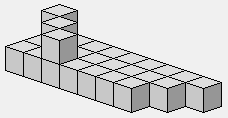
Les pyramides

0  1  1  1
1  1  2  1  1
1  2  3  2  1
1  1  2  1  1
0  1  1  1

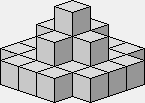
Bien que ce ne soit pas a priori obligatoire, le bon sens devrait vous convaincre de réserver une pièce particulière pour le sommet.

Épaisseur «trois»

3  3  3
    3  3  3
        3  3  3

Ce cube dont les tranches sont décalées est moins facile qu'il n'y paraît.

3  3  3
0  0  3  3  3
0  0  0  0  3  3  3

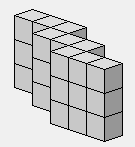
Poussons le décalage un peu plus.

0  0  0  3  3
0  0  3  3
0  3  3
3  3
3

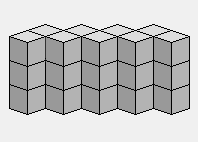
3  3  3
3  0  3  0  3
0  0  3  3  3

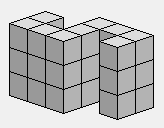
0  3  3  3
0  3  0  3
3  3  0  3  3

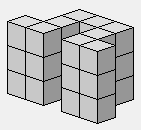
2  2  2
1  1  1
3  3  3
1  1  1
2  2  2

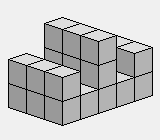
La montagne: le profil est l'idéogramme shan, ou le kanji san/yama.

1  1  1
2  2  2
3  3  3
2  2  2
1  1  1

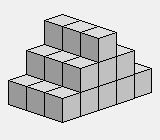
Ce prisme à base triangulaire est un des plus difficiles à obtenir.

2  2  1  2  2
2  2  1  2  2
2  2  1  2  2

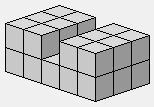
Figures élevées

7  5  1
5  5  1
1  1  1

Un vieux manuel des années 60 prétendait qu'il était possible de réaliser ce gratte-ciel. Après 50 années, je n'y suis toujours pas parvenu.

5  5  1
5  7  1
1  1  1

Par contre, si l'on place la pointe au centre, c'est réalisable.

6  5  1
5  5  1
1  1  2

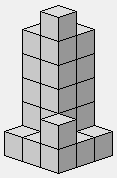
Voici un autre gratte-ciel, un peu moins haut.

0  0  3  2
0  7  5
3  5
2

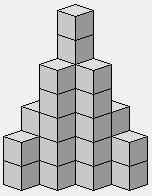
Un genre de navette ou d'aile volante.

0  0  0  0  0  1
0  0  0  0  2  1
0  0  0  4  3
0  0  4  5
0  2  3
1  1

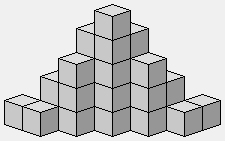
Un delta plane, ou autre aile volante.

6  4  2
4  2  1  1
2  1  1  1
0  1  1

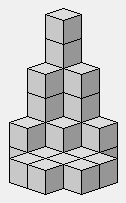
5  6  7
4  3  2

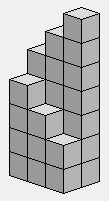
Escaliers de 2 à 7, sur deux rangées.

À classer

2  2  2  2  2  2  2
2  2  2  2  2  2  1

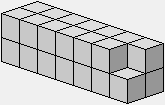
Un prisme carré de 2×2x7 n'est pas possible, mais on peut l'approcher.

2  1  1  2  1  1  1
2  1  2  2  2  2  2
2  1  1  2  1  1  1

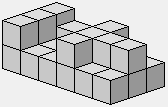
Tombe avec croix couchée

2  1  2  1  2 
3  2  2  2  2 
2  1  2  1  2 

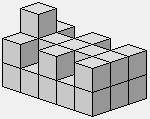
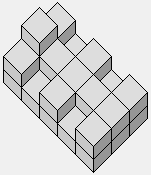
Insecte (machin à six pattes)

2  2  2  2  2  2  2  2  1
1  1  1  1  1  1  1  1  2

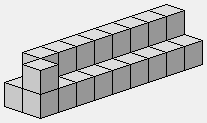
Cornière de 9×3, soit un parallélépipède d'un triangle carré de côté deux. Ce n'est pas parfait, inversion pour l'un d'eux.

3  3  3  3  3
2  1  1  1  2
1  1  1  1  1

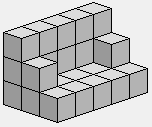
0  0  0  1  1  1
0  0  0  1  1  1
2  2  2  1  1  1
2  2  2
2  2  2

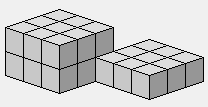
Deux dalles carrées qui se touchent.

0  0  0  0  2  2
0  0  0  2  2  1
0  0  2  2  1
0  2  2  1
2  2  1
2  1

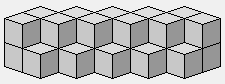
Prisme triangulaire en escalier

4  2  2  1
2  2  2  1
2  2  2  1
1  1  1  1

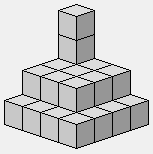
2  2  2  2
4  3  2  2
2  2  2  2

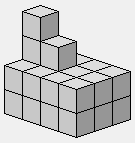
2  2  2  2
4  3  2  2
2  2  2  2

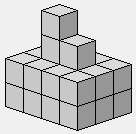
Variante du précédent

1  1  2  3  4  3  2  1  1
1  1  1  1  1  1  1  1  1

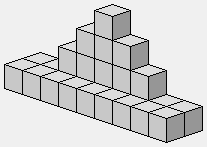
5  2  2
5  2  2
5  2  2

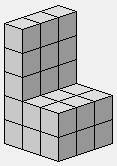
Une sorte de chaise.

2  1  1  1  1  1  2
2  1  1  1  1  1  2
2  1  1  1  1  1  2

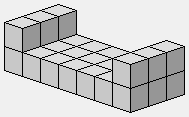
2  1  1  1  1
1  1  2  2  1
1  2  2  1  1
1  2  1
1  1  1

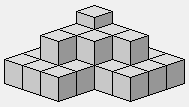
4  3  2  3  2  3  2  3
3  *

Attention: le * indique un empilement de deux cubes aux deuxième et troisième niveau (le rez-de-chaussée n'existe pas).

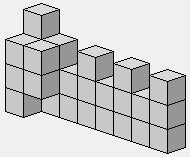
2  2  2  2
2  2  2  2
2  2  1  1
2  2  1

Deux variantes

A. Le Soma incomplet…

Il est possible de ne pas utiliser les sept pièces. Combien de figures plates (c'est-à-dire d'épaisseur 1) est-il possible de construire en n'utilisant qu'un nombre restreint de pièces? Le bon sens recommande l'élimination des pièces 5, 6 et 7.

1  1  1  1  1
1  1  1  1  1
1  1  1  1  1

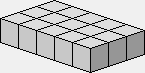
Ce sera plus simple en commençant par un rectangle de 5×3 et en déplaçant une seule pièce pour obtenir les trois figures suivantes.

1  1  1  1  1
1  1  1  1
1  1  1
1  1
1

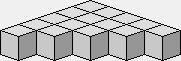
Un triangle demi-carré de 5 de côté.

0  0  1  1  1  1  1
0  1  1  1  1  1
1  1  1  1  1

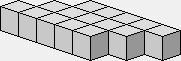
Un parallélogramme de 5×3.

0  0  1  1  1
0  1  1  1  1  1
1  1  1  1  1  1  1

Un trapèze de bases 7 et 3 et de hauteur 3.

0  0  1  1  1  1
0  1  1  1  1  1
1  1  1  1  1  1

Un trapèze rectangle de bases 6 et 4 et de hauteur 3.

Tentons les volumes simples. Comme toutes les figures totalisent un nombre quadruple de petits cubes, il faut nécessairement ne pas tenir compte de la plus petite pièce.

2  2  2
2  2  2

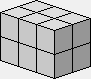
Prisme droit de base carrée de côtés 2 et de hauteur 3 (2×2×3).

2  2  2  2
2  2  2  2

Prisme droit de base carrée de côtés 2 et de hauteur 4 (2×2×4).

2  2  2  2  2
2  2  2  2  2

Prisme droit de base carrée de côtés 2 et de hauteur 5 (2×2×5). Le prisme droit 2×2×6 se montre rebelle, tandis que le 2×2×2 est impossible, sauf astuce en B.

2  2  2  2
2  2  2  2
2  2  2  2

Parallélépipède de cotés 2, 3 et 4. Souvenons-nous qu'avec le jeu complet, le prisme triangulaire est possible (voir plus haut).

La figure suivante ne comprend pas la pièce 1, puisque le nombre total de cubes vaut 24. Il s'agit en fait de cette petite pièce huit fois plus volumineuse (double dans les trois dimensions)

2  2  2  2
2  2  2  2
2  2
2  2

La figure suivante nécessite la pièce 1, puisque le nombre total de cubes est impair.

2  2  2  2  2
1  1  1  1  1

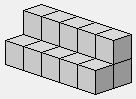
Prisme triangulaire (2+1)x5.

B. 5=6

Afin de tenter des figures qui ne sont pas possibles avec les sept pièces, on peut tenter de remplacer le 6 par un second 5 (ou l'inverse), ce qui ne résoud pas tout: ce qui n'est pas possible avec le 5 et le 6 ne l'est pas nécessairement avec deux 5 (ou deux 6). Deux 5 (ou deux 6) peuvent former le petit cube 2×2×2.

Liens

www.fam-bundgaard.dk/SOMA/SOMA.HTM (.en) site très complet avec d'innombrables figures.

www.mathematische-basteleien.de/somacube.htm (.en) parle de variantes du soma cube.